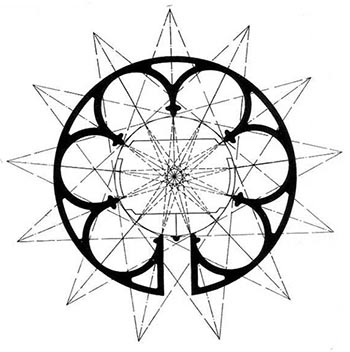
The Chartres Labyrinth:
Astronomy and Easter
Computus
Jean Le Mée (Copyright 2010)
 Introduction
Introduction
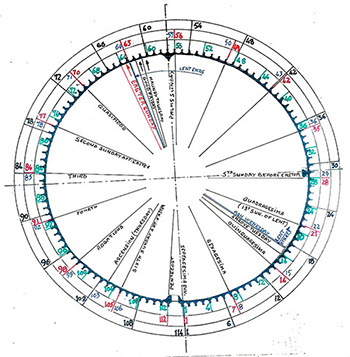
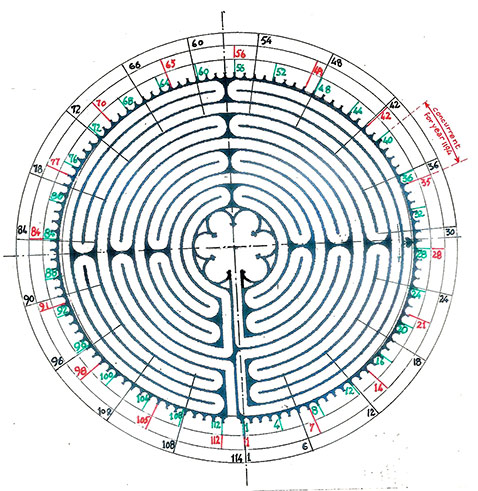
Though a number of large labyrinths were laid in the naves of several northern French cathedrals about the turn of the thirteenth century, only the one from Chartres (Fig 1) has remained undisturbed since its first installation. Those in the other cathedrals were removed, generally towards the end of the 17th century or during the 18th. What is now seen in these buildings are typically 19th century restorations made from recovered drawings (non-architectural) or what was remembered of them through tradition and passed on through word of mouth. There is therefore no absolute assurance that they represent exactly what originally existed. The difference may sometimes appear insignificant but it may nevertheless be all-important. As an example—the fact that there exist many drawings in manuscripts of the Chartres type labyrinth that do not show the characteristic crown of teeth or cogs that surrounds it. In this respect, it is worth noting that such a crown does not appear either around any other cathedral labyrinth that can be seen today, except they be modern imitations. Did they originally exist, or were there also other similar features that have simply been eliminated, perhaps judged unimportant, unaesthetic, or just forgotten when the reconstruction took place centuries later? We do not know. Again, as an example of this latter type of omission is a marking in the outer ring next to the third pillar on the south side of the nave at Chartres. Except in photographs, this mark is generally not shown at all on drawings—yet, as we shall see, it indicates an important point.
Labyrinth drawings exist in abundance in manuscripts. Yet manuscript labyrinths do not generally illustrate a specific point in the text, i.e. the text, per se, has apparently nothing to do with labyrinths. But as Doob (1990, 82-91) explains, it is there to signal a difficult process. She mentions Marius Mercator (4th century) as advocating “marking margins with a labyrinth to indicate a textual passage repaying careful study.”
No wonder then that labyrinths appear regularly in the margins of texts having to do with the computus of Easter! This does not necessarily imply thereby that the labyrinth is specifically used in the computus but that the computus is a labyrinthine thought process fraught with many difficulties. Would not therefore a labyrinth at the entrance of a great church, occupying the full width of the nave, carry similar meanings and warning? Would it not be placed there by the architect, precisely in the marginal area of the church, to remind the passerby that the very texture of the building, that is the design process that it embodies, is a complex and labyrinthine process indeed? And would it not also, at another level, remind the clerks and their students while warning the unwary that, to reach the way to the Celestial Jerusalem whose image is the choir, straight out in the distance, yet hidden behind the rood screen, one must first take the narrow, seemingly difficult and meandrous path? For is not the world itself, and even the confined world of studies, truly a labyrinthine way full of snares and minotaurs hiding in wait—temptations of the flesh and the spirit as well as distractions of the mind by the inessentials? And is not the very mystery of faith another labyrinthine experience that every Christian must undertake?
As for all medieval religious works, be they textual, pictorial, architectural, or liturgical, the reading of our labyrinth must allow at least for the traditional four levels of interpretation: literal/historical, symbolic/allegorical, moral/tropological, and anagogical, if we are to make sense of how the people who conceived it, perceived it and, possibly, used it. What is presented here belongs strictly to the labyrinth at Chartres as it can still be seen at present in the nave of the cathedral. Interestingly enough, however, as we shall see, at its most literal level it has, in reality, much to do with observational astronomy and concepts of the computus.
The Chartres labyrinth is a complex monument embedded in a complex building that emerged out of a society very different from our own. In the present article I would like to limit myself to a single aspect of its literal meaning. The thesis here is that this labyrinth, besides possessing the potential for a multitude of uses and meanings that we shall subsequently consider, is a calendrical calculator that can be used to mimic sun and moon relationships, i.e. an astronomical abacus or analogue computer of sorts. It can be used to readily demonstrate the mechanism of moon phases, eclipses and other astronomical events, as well as their inter-relationships and the determination of their dates. In the second part of this work we shall also see that its structure is such that it can be turned into a digital computing device for calculating not only the date of Easter in the Julian calendar, one of the greatest challenges for the computists of the Middle Ages, but also all the moveable feasts of the liturgical year of the Julian calendar.
Its potential as an educational tool to teach these concepts, as might have occurred in the schools of Chartres, and its suitability to serve as an aid in understanding and performing the Easter computus will be explored.
1. Calendrical Aspect of the Chartres Labyrinth
There are obvious clues in the numbers involved in the labyrinth design which point directly to the possible use of the labyrinth for calendrical reckoning (Fig 1)
-
There are 11 rings in the labyrinth path, a number equal to the difference between the number of days in the solar year (365) and the lunar year (354).
-
The labyrinth is clearly divided into four quarters and in each quarter there are seven hairpin turns for a total of twenty-eight: four respectively the number of seasons in a year and of years in a leap cycle; seven, the number of days in a week; twenty-eight, the number of moon phases in a lunar month, as well as years in the solar cycle.
-
Geometrical studies (Kritchlow, 1982, 100) have shown that the design of the rose in the center of the labyrinth is based on a 13-pointed star (Fig 2). Now 13 is the number of lunations in the solar year (13 x 28 = 364).
-
The crown of teeth that gives the labyrinth at Chartres the aspect of an enormous gear includes 113 such teeth or cogs and therefore 112 in-between spaces which, for convenience, we shall refer to as “cups.”
Further we note that the number 112 contains the factors 56, 28, 16, 14, and 7, numbers important in calendar work. Coincidentally the cycle of Easter in the liturgical year comprises 16 weeks beginning with the Sunday of the Septuagesima and ending with the Saturday before Pentecost, i.e. 16 x 7 = 112 days. Adding the Sunday of Pentecost, we obtain 113 days.
We should also notice in the labyrinth design that the space left empty in the circumference to provide for the entrance path has the exact geometric value required to accommodate another tooth with its two adjacent cups, bringing the total number of cups and teeth around the circumference to 114. This number 114 is remarkable from the astronomical viewpoint, since it is divisible by 6 to yield 19, the number of solar years in the Metonic cycle where the number of solar and lunar months forms integral numbers (228 and 235, respectively).
-
There also exists a marker or sign in the outer ring of the labyrinth(1) next to the pillar of the south aisle. It is clearly a deliberate piece of design, quite visible in situ and on photographs (Fig. 1), though, interestingly, rarely if ever seen on drawings. Counting the cogs around the labyrinth, starting at the left of the entrance with 1, we end up at 84, just at the marker, with 29 more cogs to go back to the right of the entrance. If we count the cogs anticlockwise from the entrance, the marker is at cog 30 and there are 29 cups in between. Furthermore, if we include the ½ cup at the entrance, the number of cups becomes 29½. The number 29 ½ is the average number of days in the lunar month, 29 and 30 being the number of days in alternate months of the lunar year.
It should also be remarked that (84 x 4) / 3 = 112 so that the marker indicates a ¾ turn clockwise around the labyrinth. In addition, 84 + 4 (112) = 532, i.e. after 4 ¾ turns we have gone through 532 cups, which is the number of years after which the dates of Easter Sundays repeat in the Julian calendar, as explained later.
2. Astronomy in the Twelfth Century
Before proceeding any further here, it might be useful to consider briefly the state of astronomical knowledge in Western Europe towards the end of the 12th century, at the time when these large floor labyrinths appear in cathedrals.
When thinking of early medieval astronomy one naturally thinks of what had been kept from the Greeks and passed on through by the Romans before the influx of the Arabic contribution that will really develop from the 13th through the 15th centuries. This generally consists of some meager, unsystematic leftovers in the classical quadrivium filtered through encyclopedists such as Macrobius, Chalcidius, and particularly Boethius. However, as McCluskey (1998, x-xi) has shown, this geometrical astronomy, providing a framework for the cosmos, was only part of the wider tradition of astronomical knowledge. Besides it, he distinguishes three other areas:
One divided the year by observing the sun; another computed the date of the Easter
Full Moon; the third determined the time for monastic prayers by watching the course
of the stars… Most of these astronomies were practical; they sustained the communities
in which they flourished and reflected and reinforced the values of these communities.
It would be wrong, however, to think that these astronomies existed side by side, separately, and served independent and isolated communities. Rather, they were quite well integrated and formed part of a culture in which all members of that culture shared, to a greater or lesser extent depending on their own level of education.
These practical astronomies are indeed very ancient, going back in time for millennia. As some scholars have shown over the last fifty years or so, chief among them Alexander Thom (1967), Gerald S. Hawkins (1993) and, more recently, Robin Heath (1998) the megalithic people in western Europe who built the prehistoric monuments to be found primarily in Britain and Brittany “over a period of at least two thousand years from about 3500 BC” possessed a refined knowledge of observational astronomy particularly concerning the Sun and the Moon.
Of direct relevance in our case, we notice that the Aubrey Circle at Stonehenge comprises 56 postholes. Now 56 is half of 112 so that whatever can be achieved with a circle of equally spaced 56 markers can certainly be achieved with one of twice that number. This means that the conclusions reached at Stonehenge regarding the Aubrey Circle can be applied mutatis mutandis to the crown on 112 cups of the labyrinth of Chartres. Heath (1998, 233) suggests as much.
3. The Labyrinth as an Analog of Celestial Events
3.1 Principle
As we have just noted, there are obvious analogies between the structure of the outer ring of the Chartres labyrinth and the Aubrey circle at Stonehenge. There are also obvious differences between venues. For one, Stonehenge is a monument installed in the open, on a vast plain and, obviously, designed for direct observation of Sun and Moon in real time, lasting for years. In other words, it is an observatory. The Chartres labyrinth is confined to the nave of the church with no obvious means of observation of celestial occurrences in the heaven of this Earth. However, as such, it formed part of a complex of cathedral schools. It would not be possible or realistic to operate such an “analog computer” for years on end in the middle of the space devoted most of the time to other purposes. This reinforces the idea that the labyrinth of Chartres, as far as its use as an astronomical device is concerned, was not for direct observation but, most probably, for what in today’s educational jargon is referred to as an “experiential learning tool.” One can readily imagine students representing Sun, Moon, Earth, and the planets learning the celestial dances to assimilate their astronomy or a scholar contemplating the structure of the labyrinth as one consults a vade mecum and rehearsing in his mind the celestial dance or the computus of Easter. For, as Mary Carruthers (1998) has shown, ecclesiastical and particularly monastic buildings were used as mnemonic devices for meditation and rhetorical purposes—a topic that we explore elsewhere. This is not, of course, the only use of the labyrinth but is, from this particular viewpoint, one of the most convincing explanations for its structure and location.
Considering the labyrinth itself we turn our attention to its periphery of 112 cups, 113 cogs, and a space at its entrance able to accommodate an additional cog so that the numbers 112, 113, and 114 will be available for our computation.
The first step is to see how it can be made into a calendar based on Sun and Moon motions. We may start here by following R. Heath in his Stonehenge analysis, noting, however, that with three numbers rather than one, namely 112, 113, and 114 versus 56 more precision and possibilities may be opening for Chartres.
We begin by determining the cardinal directions. In the case of an actual observatory such as Stonehenge, these will be the actual directions of north, south, east and west. In our particular case, however, the orientation of the labyrinth within the church can, and will be different since first, the church is not geographically oriented east-west and second, the point is not direct observation but understanding of the movements of Sun, Moon, and the zodiac with respect to Earth and,one would think, their relations to the liturgical calendar.
In the actual situation, Sun, Moon, and other celestial bodies rise and set at different points on the horizon as the year progresses. Such points are characterized by their azimuths. These bodies reach various heights above the horizon, known as elevations. However, the azimuth of their maximal elevation is constant and the same for all of them, namely straight south (azimuth 180 degrees). Knowing that point and given the center of the circle of observation, the north-south direction and the east-west direction are readily obtained in the field.
In the case of the labyrinth enclosed in the space of the nave, the east—the spiritual east, that is—is the direction of the apse, of the main altar, whereas the west would be that of the entrance. The south would be to the right and the north to the left of the axis of the building pointing east.
Having thus set up the cardinal directions, the points of occurrence for equinoxes and solstices can be positioned around the labyrinth and, with them, the months of the year and the houses of the zodiac.
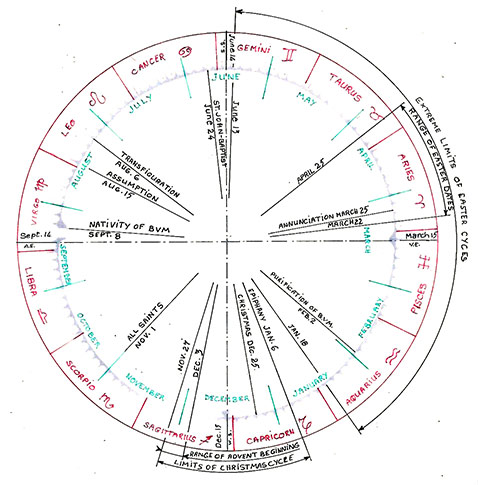
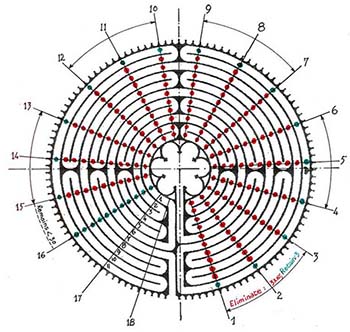
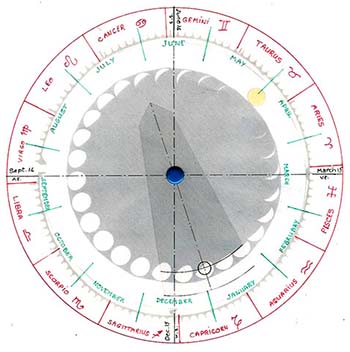
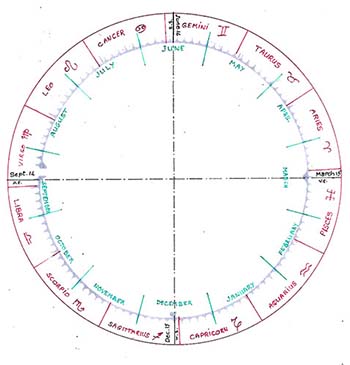
In the Massa Compoti (Van Wijk: 1936, 79, verses 288 – 289) Alexander de Villa Dei(2) gives the dates of the solstices as June 14 and December 15 and the equinoxes as March 15 and September 14 respectively. Since the Massa was composed in 1200 when the labyrinth was laid down, it is reasonable to assume his dates to be known at Chartres at the time. However, to set our calendar within the zodiac, we must use the dates used in the computus, i.e. March 21. The result is that the moon age calculated would be that of the “ecclesiastical moon” rather than the actual moon. To this end, we lay out the months based on the actual dates of the solstices and equinoxes. We then give each month its proper length.(3) Thus, for example, at the entrance of the labyrinth (the west), the axis of the path next to the entrance path itself represents the east-west cardinal direction. We shall therefore identify that point on the labyrinth circumference, i.e. cup #1 (Figure 3), as September 14 while the point on the same axis but to the east of the labyrinth will be labeled March 15. Similarly for the solstices on the north-south axis, we shall mark the summer solstice (north side) June 14 and the winter solstice (south side) December 15. The days and months can then be distributed around these dates in terms of cups as shown in(Fig 3).
The Massa Compoti states further that the sun always enters the signs on the fifteenth day of the calends of each month. Van Wijk(4) (1936; 75, verse 120; com.100) comments that this would correspond to the 17th or the 18th of the month. We can now therefore mark out the houses of the zodiac on the labyrinth. The signs can then be assigned. It is important to distinguish zodiacal signs from constellations bearing the same name. Due to precession, in the geocentric view, the line of the equinoxes appears to move in a counter-clockwise, slow motion against the background of the zodiac. The rate is 1o every 72 years which translates into a whole zodiacal house (30 o) every 2,160 years. Some two thousand years ago, the constellation of Aries, for instance, was within the sign of Aries. It is now in the sign of Taurus. However, the place occupied by the constellation of Aries two thousand years ago—roughly the first 30 o of the zodiac, eastward (counterclockwise) from the vernal equinox—though now occupied by the constellation of Pisces is still called Aries. This way of labeling the houses of the zodiac, still used today by astrologers, was also used by the computists of the Middle Ages.
The Moon goes around the zodiac in about 27 1/3 days, i.e. close to 13 degrees per day and around the Earth in about 29.5 days. The whole number in days for a lunation, 28 days, can therefore be assumed and we note that there are 13 lunations in a solar year.
What the Moon does in one lunar month, the Sun does in one year. In other words, from the Earth-centered viewpoint, the Moon appears to move very close to 13 times faster than the Sun. This movement of Sun and Moon against the zodiac is in reality an apparent “slippage,” i.e. both luminaries move daily with the zodiac and in the same direction but both lag each day with respect to the same zodiac—the Sun by a little less than one degree, the Moon by a little more than 13 degrees. The net result is therefore, for the Moon, a lag of a whole turn per lunation or of 13 such whole turns for the year while it amounts to one turn for the Sun. In other words, Sun and Moon retrogress, or move in a counterclockwise direction with respect to the zodiac. Since the zodiac indicates the month and the seasons with a convenient starting point at the vernal equinox, the position of the Sun with respect to the zodiac will indicate the date. Its representation will be a calendar. The relative position of the Moon will allow for determining the phases and the type as well as the date of the eclipses and even of the tides (Wallis, 1999, 82-85, 307-312).
This retrogressive motion of Sun and Moon can be replicated on the dented periphery of the labyrinth by using a sign for the Moon and one for the Sun and moving them, for the Moon, 1/28 of a turn daily, i.e. 112/28 = 4 cups a day and, for the Sun, the same amount of 4 cups every 13 days. Alternatively one can say that for every whole turn of the Moon sign, the Sun sign should move by 1/13 of a turn or 112/13 = 8.61 cups. To get an integral number of either 8 or 9 cups, the combination giving the closest approximation would be 5 sets of 8 cups plus 8 sets of 9 cups for a total of 112.
Some refinements using either numbers 113 or 114 can be introduced but this is not necessary to understand the principle.
Of course, as previously explained, the experiment need not, and, in fact, could not be carried out in real time. It would, however, be simple and easy and, from a teaching/learning viewpoint, enlightening and efficient, to convey concepts of astronomy that may be difficult for students to master otherwise. We shall come back to this point subsequently.
3.2 Prediction of the Moon Phases
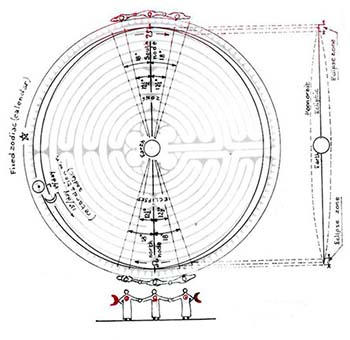
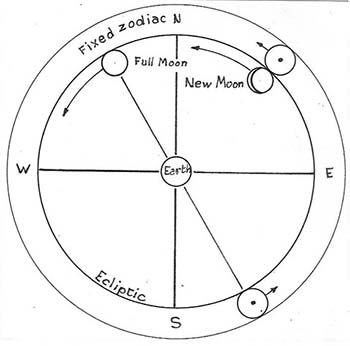
A New Moon occurs when the Moon, from the Earth viewpoint, is passing in front of the Sun(Fig 4). Then it is lost to sight in the full glare of the Sun and therefore not visible. Similarly, a Full Moon occurs when the Moon is at the opposite point of the ecliptic with respect to the Sun. Then it is fully lit by the Sun.
In our analog(5)
(Fig 5) for a new Moon the signs for Sun and Moon would be together on the same radius at say Taurus, in the zodiac; for a full Moon, they would respectively be at opposite sides of the zodiac, e.g. for the Sun in Taurus the Moon would be in Scorpio. The Moon phases can be deduced from the relative geometry of Sun and Moon signs with respect to Earth (center of diagram). If the Moon sign is in Capricorn (small circle shown within the Moon phases) and the Sun in Taurus as shown, then the phase is seen to be gibbous and waning from full to new Moon as the Moon sign moves counterclockwise. When the Sun is in Leo, the Moon would be waning in Taurus, and waxing in Scorpio.
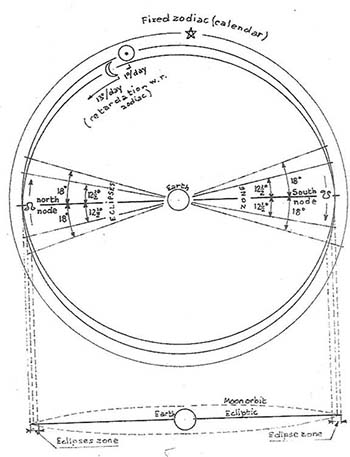
An eclipse is the partial or complete obscuring, relative to a designated observer, of one celestial body by another. The Moon orbital plane is inclined at some 5½ o to the orbital plane of the Sun (ecliptic).
The intersection of these two planes constitutes the axis of the lunar nodes, the lunar nodes being the points where the orbit of the Moon itself crosses the plane of the ecliptic.
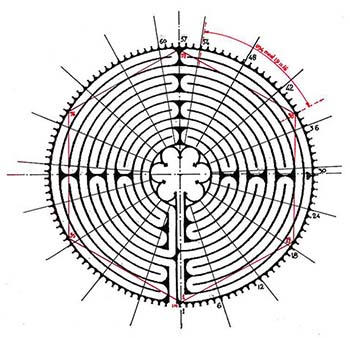
When Sun and Moon are simultaneously on the nodal axis, Sun, Moon and Earth are aligned in a straight line and an eclipse occurs. If both Sun and Moon had a common orbital plane, a full solar eclipse and a full lunar eclipse would therefore take place every lunar month—a solar eclipse at the new Moon, a lunar eclipse at the full Moon. Due to the inclination of the planes, however, Sun and Moon must be within a zone, on either side of that axis, of 18 degrees for a lunar eclipse and 12.5 degrees for a solar eclipse to occur (Fig 6) (Heath, 2001, 20). The phases of the Moon will then tend towards a Full or a New Moon respectively. These eclipses may be partial or full—full on the axis itself, partial otherwise. The nodal axis rotates in a clockwise direction with respect to the zodiac and takes 18.61 years to return to the same point on the ecliptic.
On our model, i.e. the labyrinth (Fig 7), we therefore dispose two lunar node markers, opposite one another, and define two sectorial zones of 12.5 and 18 degrees on either side of them respectively. In real time, these markers would move at the rate of one turn for 18.61 years. Obviously a slow process. In our simulation, since one year is marked by a complete revolution of the Sun sign around the labyrinth, it means that this Sun sign will achieve 18.61 revolutions for one of the nodal axis. The Moon sign would therefore move by 18.61 x 13 = 241.93 turns, i.e. 242 times faster than the nodal axis. In other words, if the Moon sign would take one minute in our simulation for a complete revolution, the nodal axis would take 242/60 = 4 hours approximately. To be practical, the demonstration of eclipse occurrences would therefore have to be done when the Moon and Sun signs are in the vicinity of the season of eclipses, i.e. the sectorial marked zone mentioned above. Letting the Sun and Moon sign move through, say, 40 degrees would take 1/9th of a year, i.e. 1/9th of a complete turn of the Sun sign. In terms of cup numbers, for 112 of the Sun sign, the node signs would move by a little more than 6 cups (112/18 = 6.22 cups, i.e. 6 2/9 cups). Of course, to simply demonstrate the mechanism of the eclipses, one does not need to have the orbital velocities in perfect proportion.
3.4 The Games
One may wonder how such a model might have been used in a place such as the Cathedral of Chartres. One idea that readily comes to mind, given the setting of the Cathedral in an academic context where the liberal arts and astronomy, in particular, were held in high esteem, was that students might have been presented with games that would reproduce the evolution of the celestial bodies in the heavens. This would make the intricacies of astronomy more palatable and memorable to them by exploiting the traditional and effective way of learning with one’s whole being to help memorization, to which we previously alluded (Leclercq, 1982).
Fulbert, who was a teacher and chancellor of the schools of Chartres at the turn of the eleventh century and later bishop of Chartres (d.1028), composed a short poem to help his students memorize by heart the essential of the computus, i.e. the calculation of the date of Easter. The poem includes a whole section on the Signs of the Zodiac, the months, the days, the hours, and ends with a short piece on the astrolabe (Behrends, 1976, 259ff). Parts of this poem are included below in Sections 10.4.2 and 10.5.
The re-enactment of the motions of the heavenly bodies by students would therefore be a natural way of teaching astronomy in the schools of Chartres(6) —in a sense, building an analog computer with human beings.
Perhaps carrying a simple sign, symbol of a particular heavenly body, or perhaps on solemn occasions, dressed up in a rich costume embroidered with that sign or symbol (Fig 7a), students would be instructed to perform the cosmic dance of Sun and Moon. So one of them would stand for the Moon going around the periphery of the labyrinth; another for the Sun, also going around the periphery but at a majestic pace 1/13th of that of the first. Yet another might keep track of the movements, positioned in the center, and move himself by one notch (one spike of the 13-pointed star implicit in the central six-petal rose) for every turn of the Moon or spin on himself to represent the earth in its relative motion with respect to the fixed zodiac. Of course, as previously explained, in such a game, it could not be a question to perform the motions in real time—28 days to go around the labyrinth! What would be essential is to make evident to the students the relationship between Sun and Moon movements with respect to the zodiac. Again, as mentioned previously, sets of 8 or 9 cups would be marked ahead of time so that the Sun would go through one such set as the Moon completes one whole turn.
It is the relative geometric position of Sun, Moon, and Earth that is determinative for the phases of the Moon. To readily make this evident one can imagine 28 students dressed up with a nice black velvet costume bearing on the chest and the back the image of one of the 28 phases of the Moon and moving together around the labyrinth at the same pace and in concert with the Sun sign. Then whatever image of the Moon phase the Moon sign happens to be next to would indicate what the phase actually is (Fig 5)
Similarly, for the eclipses, we need to materialize the two lunar node markers previously mentioned. Two students bearing the sign of the nodes on their back and chest can represent them. And to define the sectorial zone of 12.5 and 18 degrees respectively on either side of them, two other students can be positioned next to each of the node-sign- bearing students (Fig 7b) on the periphery of the labyrinth spanning an angle of 12.5o. By extending their external elbows, they would indicate the extent of the 18o angle. They would carry, either on their backs or chests, a Sun sign to indicate the limits of solar eclipses and on their external elbows, a Moon sign for the limits of the lunar eclipses.
One could see them hardly moving around while the Sun goes around 18.61 times faster than they do and the Moon, 13 times yet as fast as the Sun, i.e. 242 times faster than the nodal axis! Obviously the exercise would have to be staged close to an eclipse occurrence to demonstrate the mechanism and so as not to consume an excessive amount of time, should proportionality of time be respected. For purposes of demonstration and learning, the time scales of each luminary would have to be scaled appropriately. In any case, the best way to keep all this moving in proper proportion would be through music, each celestial body moving according to its proper time or beat, in its own partition—the Harmony of the Spheres.
This, of course, would be an occasion to “incorporate” in the literal sense of the word, another discipline of the curriculum with astronomy, geometry and the calendar, and thus “cover” the whole quadrivium.
Of course many other games for learning could be devised as we shall see when considering the determination of the date of Easter.
There is no indication in the record that anything similar to these games ever occurred at Chartres but it would nevertheless seem to be a natural outcome for such a marvelous instrument placed in a setting where the learning of astronomy was in honor when it was erected. In any case, as previously mentioned, it may have been done only mentally as a mnemonic technique to assimilate and remember the complexities of astronomy and the computus.
4. Need for a Long-range Prediction of the Date of Easter
Liturgically, Easter is the outcome of a series of events, observances and feasts. Its date, therefore, which is variable and depends on the lunar phases within a narrow window in the solar calendar, has to be known well in advance so that adequate preparation may be made in due course since all these observances need to move accordingly.
As Bede’s work De temporum ratione (Wallis, 1999)shows, the computus essential purpose was to establish a church calendar so that the date of Easter could be accurately determined and the liturgy of the year set up well in advance. Major feasts such as Christmas and Easter have times of preparation of more than forty days (e.g. Advent and Lent) and extensions onwards equally lengthy (e.g. Epiphany, Ascension, Pentecost).
5. Definition of the Date of Easter
The definition of the date of Easter is deceptively simple. “Easter shall be the first Sunday after the first full moon occurring on or after the vernal equinox,” declared the Council of Nicæa in 325. However, vernal equinoxes and Full Moons needed to be known in advance to get ready for the celebration on Easter Day and this was not as simple as it appeared. The fact that various sects or congregations had their own methods and habits was not to be easily changed either. Furthermore the calculation itself presented challenges that were not to be readily overcome. The small discrepancy between actual and tabulated values that were inappreciable on a yearly basis became, over the centuries, a matter of several days. As Heilbron (2001, 36) mentions, by the year 800 the accumulated discrepancy amounted to 3.70 days since the Council of Nicæa and the vernal equinox was coming on the 17th or 18th of March rather than the 21st as assumed by the Tables. In 1200 Alexander de Villa Dei gave the date of the vernal equinox as March 15th, as we saw.
6. The Julian Calendar
The Julian calendar was in force during the whole medieval period, from its institution under Julius Caesar in 45 BC to its replacement by the Gregorian calendar in 1582 under Pope Gregory XIII—a calendar under which we still operate.
The Julian calendar is a solar calendar and follows the seasons fairly accurately. It includes 365 days with a leap year of 366 days every four years like the Gregorian. However, since the year in actuality is 365.2422 days long, each Julian year exceeds the astronomical year by 0.0078 days or 11.2 minutes.
The discrepancy causes the equinoxes to retrogress through the Julian calendar by roughly three days every 400 years. This, of course, can run havoc in the computation of Easter if uncorrected, and it did. One will indeed have to wait until the Gregorian reform of 1582 for this correction to occur by which time the discrepancy had grown to more than 12 days.
7. Solar and Lunar Cycles. The Metonic Cycle
One of the difficulties presented by the calculation of the date of Easter results from the fact that it depends on two cycles, one of the Moon and the other of the Sun.
Observation, however, shows that, every 19 years, dates in the solar years and the phases of the Moon repeat in the same sequence. Modern astronomers call it the Metonic Cycle. This periodic re-synchronization of Sun and Moon cycles means that, within this period of 19 years, the number of solar months and lunar months are whole numbers and contain (to within one day) the same total of days.
Three points must be noted here:
The first is that there is an excess of one day in the lunar cycle that must therefore be dropped to have the cycle repeat more exactly. The Moon, or more accurately the “Moon Age” must “jump” or skip one day at every cycle. This is known as the saltus lunae (the moon jump).
The second point to be noted is that the intercalation of a day in the leap year in February has the effect of making the Moon one day older after this intercalation. This would therefore affect the date of the Easter Full Moon. To compensate, the Moon Age on the first of March is maintained at what it was previous to the intercalation.
Thirdly, therefore, every 19 years both Sun and Moon return very closely to their same respective position on the ecliptic, i.e. the Moon as calculated will be in the same phase on the same two dates 19 years apart. It is then easy to compile a table of Moon phases for succeeding cycles. What does not repeat, however, from each 19-year cycle to the next is the sequence of the days in the week within the cycles.
8. The Cycle of the Weeks
Having a system to match dates and Moon phases within a 19-year cycle—the Metonic Cycle—we now look for a cycle that would match the days of the week with the Metonic Cycle, a topic of crucial importance for determining the date of Easter Sunday.
The sequence of the days in the week, Sunday through Saturday, keeps repeating throughout the year. Since the week has seven days, if each year had 364 days, everything would be simple since 52 x 7 = 364, the year would have exactly 52 weeks and each year would have the same sequence of dates and week days, years without end! Unfortunately common years have 365 days and leap years, 366, this every four years. So, for a succession of common years, the days of the week shift by one day every year on the 1st of the year. The pattern would repeat after seven years, were it not for the presence of a leap year every fourth year which changes the cycle to one of 28 years, since 7 x 4 = 28. Within a 19-year cycle there are therefore 19 possible arrangements of dates out of these 28. The possibility of having the same dates coinciding with the same days of the week will therefore occur every 28 x 19 = 532 years. This corresponds, in terms of cups, to 43/4 turns clockwise around the labyrinth from entrance to the point indicated by the marker mentioned earlier.
We are now in a position to consider the computus of Easter in the Julian calendar. From this we will then be able to see how the design of the labyrinth may be used as an aid in the computation.
9. The Computus or an Algorithm for Forecasting the Date of Easter in the Julian Calendar
9.1 Principle
For a Full Moon to occur on or after the Vernal Equinox,(7) the New Moon, i.e. the beginning of the Lunar Month that will contain that Full Moon, must begin no more than 14 days before the equinox. That New Moon is the first of the lunar month and therefore the real point of departure.
By direct observation, the New Moon would be determined by the appearance of the first sliver of the crescent. However, as previously mentioned, the Moon considered in the computus is not the actual moon but one that is computed—the Ecclesiastical Moon—and the equinox is not the actual vernal equinox but the date of March 21st.
The Moon phase or its “age” is indicated by the number of days after the first New Moon. From the knowledge of the age of the Ecclesiastical Moon on March 21st one finds how many days later the Full Moon occurs, the so-called Easter Limit, March 22nd being the earliest acceptable limit for Easter.
Knowing the Easter Limit, the next step is to identify the Sunday following that day. Here, some sort of universal calendar is needed for matching the days of the week to the dates. These determinations can be done through a system of regulars and epacts.
The system of regulars and epacts, which appears to be of Greek origin, was worked out in Bede’s De Temporum ratione (chapters 20-22).(8) The monthly lunar regular is a number representing the age of the Moon on the first day of each month during the first year of the nineteen-year Metonic cycle. Successive years in that cycle are related through the lunar epact, the days in excess of the solar year over the lunar year (specifically 11 days per year). Year one of this cycle was chosen so that the Moon on March 22nd be new. The yearly lunar epact was then null (i.e. zero). The implication is that “the annual lunar epacts noted for the various years in the nineteen-year cycle specifically stand for the age of the Moon on March 22nd ” (Bede, chapter 50).(9)
The monthly lunar regular added to the annual lunar epact(10) will yield the age of the Moon on the first of the month of any subsequent year in the 19-year cycle, e.g. the age of the Moon on January 1st of the second year of the 19-year cycle will be: 9 + 11 = 20.
As was explained previously, in the Metonic 19-year cycle, the phases of the Moon repeat at the same date from cycle to cycle. To be useful in the determination of Easter Sunday, dates must be matched, however, with the days of the week. This is done through the 28-year solar cycle. In this cycle, one works by analogy with the Metonic cycle with solar regulars and solar epacts, the latter also known as concurrents.(11)
The solar or monthly regulars measure the “weekday distance” between the weekday of the first of each month and the reference week day of March 24th.(12)
The solar epact or concurrents are shifts in weekdays due to the previous cycle. They are represented by numbers assigned to each of the 28 years of the solar cycle.(13) To find the day of the week for the first of any month, we simply add the solar regular for that month to the concurrent of the corresponding year and translate the resulting number into a weekday, e.g. suppose the concurrent of the year is 5, since April has a solar regular of 1, the sum of the two is 6, corresponding to a Friday. (Sunday = 1; Monday = 2; Tuesday = 3; Wednesday = 4; Thursday = 5; Friday = 6; Saturday = 7 where the first and last day are included in the count).Having this for every month it is easy to find the weekday for any date within that month. For instance, if April 1st is a Friday, April 9th will be a Saturday.(14)
9.2 Algorithm
We do not know exactly what kind of algorithm the Chartrians used for their determination of the date of Easter. However, given the widespread popularity of Bede’s De Temporibus and the testimony of Fulbert’s poem “A Compendium of the Computus” which accords with Bede’s account, there is every reason to believe that, when the labyrinth was set in the nave of Chartres, less than two centuries after Fulbert, the same method of computus was still in vigor (Wallis, 1999 and Behrends, 1976).
A careful reading of Bede can be translated into the following algorithm for the determination of the date of Easter for any year in the Julian calendar.
Algorithm Example
1. Choose the year Y. A.D. 1194 A.D.
2. Calculate Golden Number (G.N.)(15)
G.N. = (Y + 1) mod 19 (1194 + 1) mod 19 = 17
3. Calculate the Lunar epact E
E = [11 (G.N. – 1)] mod 30 E = [11 (17 – 1)] mod 30 = 26
4. Calculate the Easter limit L
L = (March 22 + 14) – E L = (March 22 + 14) – 26 =
If L < March 22 March 10
Then L = L + 30 L = March 10 + 30 = April 9
5. Calculate the concurrent or solar epact C(16)
C = (Y + Y/4] + 4) mod 7 C = (1194 + 298 + 4) mod 7 = 5
6. Determine solar regular R
If L in March, R = 5
If L in April, R = 1 R = 1
7. Calculate week day for 1st of month D
D = C + R D = 5 + 1 = 6 (Friday)
8. Calculate day of week for Easter limit
DL = D + (L – 1) mod 7 DL = 6 + (9 – 1) mod 7 = 6 + 1 = 7
(Saturday)
9. Calculate date of Easter Sunday SE(17)
SE = L – DL + 8 SE = April 9 –7 + 8 = April 10
Behrends (1976, 257, n. 147) notes that the fundamentals of this kind of calculation were widely known in the early Middle Ages. Indeed Bede (1990, 317) himself said so, as we have previously seen.
Bede’s work was certainly directly familiar to the Chartrians for the chapter library appears to have possessed at least two copies of his De temporum ratione. Furthermore, with scholars such as Thierry of Chartres at the helm of the schools in the 1100’s and his well documented interest in scientific matters and cosmology in particular, there is no doubt that the best learning to be had regarding the computus was present at Chartres in the twelfth century.
10. Labyrinth and Easter Algorithm
How can the Chartres labyrinth help in its implementation though?
The solution resides in some of the remarks regarding the structure of the labyrinth by which we began. We noticed that the algorithm requires a number of arithmetical calculations to be done modulo 7, 19 and 30 and therefore divisions by these numbers while looking for the remainders of these divisions. It also requires division by 4, multiplication by 11, addition and subtraction of sundry numbers.
To us, used to hand calculators, it is less than elementary. Deprived of our calculators and left to do long divisions by hand, it already is a challenge for some of us; doing it with Roman numerals or on an abacus it is still more of a challenge. It is only in the thirteenth century, particularly through Fibonacci’s Liber abaci, that Indo-Arabic numerals were introduced in the West. Even though one has to wait a couple of centuries before their usage became widespread. However, the use of the abacus itself with its implicit concept of “place” or “position” was somewhat familiar to calculators, particularly merchants.
To the people of the Middle Ages, these were more than arduous tasks. Few were really proficient at it—they may have been able to use the tables—but understanding and performing the operations involved was certainly beyond the ken of many even among the learned. Though Bede, in the 8th century, mentions that “many in Britain can readily compute the cycles of these Paschal times,” it doesn’t seem that this was general on the continent, nor even in Britain in the following centuries (Heilbron, 2001, n. 81). That the computus remained a subject of study for many subsequent centuries had probably less to do with the Easter computation itself, the result of which could be obtained directly from tables, than with its philosophical aspect.
The question is how may the labyrinth help? We have to recall here our observations on its structure made previously, namely that it has 112 cups, 114, if we include the “missing” cog at the entrance; that it has 11 circuits; that it is divided into 4 quarters, each with 7 hairpin turns, etc. The crown of cogs around the labyrinth will be particularly useful in performing divisions and finding the results for modulus operations. As we have noticed 112 is divisible by 28 and 7 yielding 4 and 16; similarly 114 is divisible by 19 yielding 6. Dividing by 19 is finding how many times 19 (the divisor) is contained in the number we want to divide (the dividend) and, if not an exact number of times, what is the remainder. Since 19 is contained exactly 6 times in 114, this is easily marked on the circumference by its radius or the figure of the hexagon.
10.1 Obtaining the Golden Number for Any Year A.D. with the Labyrinth
The so-called Golden Number represents the rank of the year in a Metonic cycle of 19 years.
Let us take again the example of the year 1194 for which we wish to find the Golden Number.
GN = (1194 mod 19) + 1
The first operation is to divide 1194 by 19 and look for the remainder disregarding the quotient, which is kept as a whole number.
Dividing 1194 by 19 is asking how many times 19 fits into 1194. The simpler way to find out is to subtract 19 from 1194 until we are left with a number less than 19. By counting the number of times this subtraction has been done, we obtain the quotient; then the number less than 19 that remains after this operation and from which we obviously cannot extract 19 any more is the remainder and that is the result of the operation noted: 1194 mod 19.
We can remark here that any number divisible by 19 will evidently leave no remainder. Consequently, if we have a large dividend to divide by a small divisor as in the present case, the subtraction would have to be carried out many times. This can be simplified considerably by removing this divisible number with a 0 remainder from the proposed dividend, since this will have no effect on the remainder of the original operation. We have thereby reduced the division of the large dividend to a subtraction from a much smaller number.
Turning now to apply this to the labyrinth, assuming each cup (or cog) to represent one year
(Fig 8), when we have gone around the circumference exactly 10 times, we have covered 1140 years. We are therefore just missing 54 (i.e. less than a full turn) to reach 1194. To divide 54 by 19 we can therefore just go around the labyrinth counting groups of 19 cups as many times as needed to reach 54. We see that after two times only we are left with less than 19, namely 16 in our case. So the division of 54 by 19 is 2 with a remainder of 16 or that of 1194 by 19 is 10 x 6 = 60, plus 2, i.e. 62 with a remainder of 16.
Therefore: 1194 mod 19 = 16
then GN 1194 = 16 + 1 = 17.
10.2 Determining the Lunar Epact with the Labyrinth
The lunar epact has been defined as:
E = [11 (GN – 1)] mod 30
This involves a multiplication by 11 and a division by 30 to find the remainder. We may first notice here that since GN, the Golden Number, represents the rank of the year in question in the 19-year cycle, this Golden Number cannot exceed 19 and therefore (GN – 1) = 18 at a maximum and 0 at a minimum.
The first operation to perform is therefore to add that number 11 times to itself. This is where the 11 circuits of the labyrinth may prove useful. Also, noting that 19 x 19 = 361, we can divide the circle in 19 sectors with an angle of 19 degrees at the center with a negligible error. Although this last point is not essential for the calculation, it will provide a more convenient and esthetically pleasing appearance for the results (Fig 9).
Since (114 x 19)/ 361 = 6, every 6 cups cover an arc of 19 degrees. So, every 6 cups we lay a line between the labyrinth center and the periphery. Each of these lines, which need not exceed 18, cuts the 11 circuits. The total number of crossings with 18 lines is therefore 18 x 11 = 198 representing the maximum number for [11 (GN – 1)].
In the case of our example for the year 1194, the number we have to multiply by 11 is 16 so we retain only 16 such lines.
Now we must divide the number of these crossings by 30 and find the remainder. So, as in the case of the Golden Number, we shall eliminate the crossings, in the present case, by batches of 30 until we find a remainder less than 30—a technique well known on the abacus familiar to people of the Middle Ages.
A simple way to do this is to eliminate three lines at a time (red dots on figure 9), keeping one crossing for each (green dots on figure 9), so that we get rid of 3 x 10 crossings each time. We then keep progressing in this way until the number of crossings left is less than 30. We can then count this remainder and that will be equal to E, the epact.
To animate this and make it a participatory game, we can ask people to stand at the crossings (we shall never need more than 198 people!). They would easily be found in a school like Chartres in the 1200s. We then ask three rows at a time to walk away leaving just one person per row at say the periphery. The last batch will have less than three rows. People in these rows, plus those left over from the previous rows, can then count themselves out. Their number, less than 30, will be that of the epact. For 1194, that will be 26.
10.3 Finding the Easter Limit with the Labyrinth
Now the Easter limit is in sight!
Since March 22 + 14 is, in fact, April 5, we write
L = (March 22 + 14) – E as L = (April 5) – E
The circumference of the labyrinth is evenly divided into 19 batches of 6 cups each (Fig 10). We take one cup to represent one day. The Easter period being limited to
March and April will therefore occupy less than half the circumference. Though we can start anywhere on the circumference, we arbitrarily make March 1st to coincide with cup number 1, say directly at the right of the entrance to the path. Then March 22 will coincide with cup 22 and April 5, with cup 36. The marker on the south side of the path lies between cups 29 and 30. Alternatively we could make April 5th to coincide with the marker. It is simply a matter of convenience. Sticking to our first choice and our example for 1194, we gather all the members of the “epact group” next to cup 36 designating April 5th. Then, selecting one of the team members, we ask him to move back towards the March 1st cup, hopping from cup to cup, one cup for each member of the group, i.e. 26 in total.
Where he stops would be the Easter limit, if he has not passed cup number 22 (standing for March 22). Should this happen, as is the case in our example, he then must change direction and hop thirty times again in the opposite direction. Where he stops is the Easter limit. In our case he went past the cup for March 22 to the cup for March 10 and finally ended up at cup 40. Since March has 31 days, this would be (40 – 31 = 9) or April 9th. That indeed is our Easter limit.
To find the date of Easter Sunday following our algorithm, we first must determine the concurrent and solar regular for the year under consideration.
10.4 Calculation of the Concurrent or Solar Epact with the Labyrinth
10.4.1. Using the Algorithm (Fig 11)
C = (Y + Y/4] + 4) mod 7
This involves a division by 4, keeping the quotient and neglecting the remainder, and a division by 7, neglecting the quotient and keeping the remainder.
Dealing first with the division by 4, we observe that 112 is divisible by 4 and yields 28. Therefore 1120 divided by 4 will give 280, a result that we keep in mind for all further applications.
In our example for 1194, to obtain Y/4], we can then operate first on the difference of 1194 – 1120 = 74, i.e. always reducing the number to one that is less than the total number of cups around the labyrinth. We get the quotient, entire, 74/4] by subtracting sets of 4’s from 74 stopping when the remainder is less than 4. This can be obtained from the labyrinth by counting or measuring out sets of 4 cups up to within less than 4 from 74. In our particular example this will be 18 so that
Y/4] = 280 + 18 = 298.
Therefore
C = (Y + Y/4] + 4) mod 7
= (1194 + 298 + 4) mod 7
= 1496 mod 7
Again, to calculate mod 7, we want to eliminate large numbers and note, “Bedewise,” that 112 x 10 = 1120
112 x 3 = 336
i.e. adding 112 x 13 = 1456
In other words the remainder of 1456/112 is obviously 0; therefore we have to deal only with the difference
1496 – 1456 = 40
and since the remainder of 40/7 is the same as that of 1496/7 we have:
1496 mod 7 = 40 mod 7
All we have to do then is to count or measure out sets of 7’s up to 40 around the periphery of the labyrinth. We find 5 such sets with a remainder of 5, which is therefore the concurrent for the year 1194.
An alternative method that may have been favored at Chartres combines the use of the labyrinth and the recitation of the section of Fulbert’s poem concerned with the concurrents.
10.4.2. Alternative Determination of the Concurrents
Fulbert’s poem reads, in part, as follows: (Behrends, 1976, 261):
The day on which each month begins is laid out for you
in these seven little lines. Each of them contain four numbers,
and the total, twenty-eight, are distributed over the same number
of years according to a fixed pattern. These numbers are also called
the solar epacts. These are the concurrent numbers for the years:
The leap year number is one, the next years are two, three, and four;
The leap year’s is six, and the next’s, seven, one, and two;
To the leap year belongs four, while five, six, and seven are for the following.
To the leap year goes two, while three, four, and five have their own years;
When the leap year is seven, the next years are one, two, and three;
When it is five, they are six, seven, and one;
A leap year of three is followed by four, five, and six.
Note that this is a reading of Table 2 (n.12).
Since the labyrinth contains 28 hairpin turns, divided into 4 sets of 7 (Fig 12), one can assign the value of a concurrent to each of them. Reciting Fulbert’s poem as one walks through the labyrinth so that the numbers of the concurrents come up as one turns the bends, imprints in one’s memory through sound, sight, movement and kinesthetic sense, the number with the labyrinth landscape.(18) A process no doubt familiar to a Chartrian student who would meet it also in his musical education in the cathedral schola, where sound, sight, movement, liturgical gestures, smells of incense, candles, and flowers, etc. converged together to leave their holistic imprint on his memory. At the same time, following Bede’s recommendation, (Wallis, 1999, 345) the student walker can keep track with his fingers of the year’s rank within the 28-year solar cycle. (For instance again we find that the 27th turn corresponds to 5.)
Knowing the concurrent of a particular year, one can, using these techniques, determine what the concurrent is for any year in the past or future (Wallis, 1999, 342-346).Yet, even for this, one has to have a starting point—the knowledge of the concurrent for a particular year A.D. This, however, is easily determined with the help of the labyrinth.
As we have seen in note 13, the rank of a particular year A.D. within the 28-year cycle can be readily obtained from the formula
(Y – 19) mod 28
which for our usual example of 1194 A.D. means that 1194 is ranked 27th in the 28-year cycle. Fulbert’s little poem above will tell us that the answer is 5, since, reciting the poem while counting on his fingers the concurrents up to the 27th, the student hears number 5. Alternatively he can again walk the labyrinth and find out, or perhaps just look at it and visualize, the 27th hairpin turn and its associated number 5.
But how do we use the labyrinth to help in the computation of the year’s rank? Basically this is analogous to finding the Golden Number. But this time, instead of dealing with a set of 114 cups, we are going to use the set of 112, since 112 is divisible by 28 yielding 4.
Again with the same example of the year 1194 A.D. we see that if we go around the periphery of the labyrinth ten times, we cover 1120 years (40 x 28) so that the problem is reduced to that of finding (1194 – 1120 – 19) mod 28 or (55) mod 28, a much easier task.
Counting 55 cups around and eliminating 28, we are left with 55 – 28 = 27, that is the rank of the year 1194 A.D. in the 28-year solar cycle.
The next step is to determine the regular for the month we are dealing with.
10.5 Determination of the Solar Regulars
In the calculation of Easter, which always falls either in March or in April, the only thing to remember is that it will be 5 for March and 1 for April. Not a labyrinthine process here! However, if regulars are needed for other months, they can either be easily calculated as has been shown previously in the algorithm or they can be obtained from another section of Fulbert’s poem (Behrends, 1976, 259):
To each month is assigned a regular number.
To each year is affixed a concurrent number.
Their sum gives the first-of-the-month’s weekday.
Here, for the month, are the regular numbers:
Five is pleasing to March, One satisfies April,
May will have Three, while June will double these three.
One only for July, but to you August, Four are attributed.
September takes Seven, but October needs Two.
November returns to Five, December to Seven.
We won’t take January its Three, nor its Six to February.
Our student, having walked through the labyrinth, reciting the concurrents, has arrived at the center. This will be the time for him to pause in each of the six petals of the rose to recite, in each, one of the six verses of Fulbert on the regulars.
For good measure, we will ask him to also recite the other section of the poem dealing with the months and their structure as he proceeds for a second time from petal to petal, two verses at a time:
March, May, July, October in well balanced Libra
Each has six days of Nones, seventeen Calendes days
When past are the Ides, thirty-one days total.
June, April, then with September gone, November
All have four days of Nones and when the Ides are past
Eighteen days of Calendes, a sum up to thirty.
Again, February takes up four days of Nones
But, past the Ides sixteen days of Calendes
A poor twenty-eight days,
But at each leap year a ninth day gladdens it.
Each of the twelve months starts with its own Calendes
And each, in turn, counts eight days before the Ides.
Behrends (1976, 258, note 2) suggests that the contents of the present paragraph might perhaps be more easily grasped from the jingle:
In March, July, October, May
The Ides are on the fifteenth day.
The Nones, the seventh; but all besides
have two days less for Nones and Ides.
For us it is simpler to stick to the habitual way of reckoning the days 1 through 28, 29, 30 or 31st as the case may be.
Having thus reviewed the month and the number of days for each, our student should be in a position to verify his knowledge of the regulars. Whether he has been taught or has discovered it for himself, he should be made aware that each regular can be obtained by the addition of 3 to the previous one for preceding months of thirty-one days or of 2 for months of thirty days as shown in Table 1, note 10.
In possession of concurrents and regulars, the first weekday of the months is obtained by simple addition:
D = C + R
yielding a number signifying a day such as: 1 = Sunday; 2 = Monday…7 = Saturday.
The rest of the operations, as seen in the example of the algorithm, are very simple single digit additions or subtractions that are easily carried out in mind and do not require a labyrinth.
11. Labyrinth and Liturgical Year
The calendrical cycle of 52 weeks plus 1 day or, for leap years, 2, is divided into other cycles—one fixed in calendrical time for the feasts centered on Christmas and one moveable for those centered on Easter. Taken together, these two cycles form the Temporal Cycle or Proper of the Seasons. Time not belonging to these two cycles is known as Ordinary Time or Intermediate Season. There is also another cycle known as the Sanctoral Cycle or Proper of the Saints. Whereas the Temporal Cycle contains the feasts of Christ, i.e. anniversaries of the principal events of his life, the Sanctoral Cycle includes those of the Virgin and the saints, though there is a bit of overlap, some of the Sanctoral Cycle feasts being included within the Temporal Cycle.
The cycle of Christmas, and indeed the liturgical year, begins with Advent. The Christmas cycle ends with Epiphany (January 6th, the twelfth day of Christmas). The cycle of Easter begins with Septuagesima or the ninth Sunday before Easter and ends at Pentecost, seven weeks after Easter. It extends over a period of 16 weeks or 112 days. The position of the Easter cycle within the year is determined by the date of Easter Sunday.
Advent is the period preceding Christmas. It begins on the fourth Sunday before Christmas and ends December 24th. Since the dates of Sundays change each year, the beginning of Advent varies from year to year between November 27th and December 3rd. The period of Advent, however, always ends with Epiphany, January 6th, though it may be extended to the following Sunday (i.e. as far as January 13th). The Presentation of the Infant Jesus to the Temple and the Purification of the Virgin Mary after childbirth, forty days after Christmas, on February 2nd, formally ends the Nativity Cycle.
As we have previously seen, the date of Easter may vary between March 22nd and April 25th. But all the feasts that belong to the cycle of Easter are in fixed relationship with one another so that they swing, as a whole, around the calendar within the limits imposed by the date of Easter. Since, as also previously mentioned, the Easter Cycle begins with the 9th Sunday before Easter Sunday and finishes at the end of the 7th week after Easter, it cannot begin before January 18 nor finish after June 13th. This covers a period of 145 days during which the block of 112 days of the cycle will oscillate back and forth following the movement of Easter Sunday.
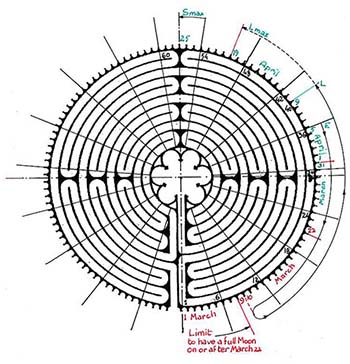
Laying the whole liturgical year onto the labyrinth (Fig 13) is helpful in visualizing the cycles in relation to one another and to the calendar, including the zodiac, providing thereby a useful tool for connecting liturgy and the seasons as well as for thinking about the mechanics of the system or meditating on its symbolism and significance. However, this way of superposing the entire liturgical year on the labyrinth lacks the precision needed for calculation since cups on the periphery of the labyrinth do not always represent the same number of days and days are represented by fraction of cups rather than whole cups.
More illuminating perhaps is to lay out the Easter cycle around the labyrinth taking advantage of the fact that it has 112 cups that can be assigned, one on one, to the 112 days of the cycle. Since 112 is divisible by 7 yielding 16, we can divide the space between cup 1, at the right of the entrance, to cup 112 at the left of the entrance, into 16 equal sectors each representing a week and each including 7 cups. If we assign cup #1 to Septuagesima (Fig 14), cup #8 will represent Sexagesima, Cup 15, Quinquagesima, etc.
With this system it is simply the dates assigned to the 112 cups that will change with the date of Easter. Once the date of Easter has been determined, as already explained, then starting by assigning that date to cup(19) #64, we lay out the relevant dates for the various feasts for that particular year by simply stepping around the labyrinth and counting our steps—solvitur ambulando!
This way of proceeding has the advantage of showing more clearly the layout of the Easter Cycle, since the arrangement of the feasts is fixed on the labyrinth. Simultaneously one can also lay out the Cycle of Christmas on the labyrinth using, for instance, the marker in the exterior-most circular path for the date of December 15th, since it is an indicator for the winter solstice, as shown in Fig. 13. In this way we have the whole Proper of the Seasons together on the periphery of the labyrinth.
This cannot have but a powerful symbolic effect, since the Proper of the Seasons represents Christ’s work of redemption: the Christmas section through His Incarnation and manifestation (Epiphany), the Easter section, by the fulfillment of the promise of redemption.
This therefore leaves the inner path of the labyrinth for ordinary time. Here we see the exterior crenellated circle of the labyrinth containing the turbulent turns and twists of the inner path from spreading out like the innards of a disemboweled animal. It shows the whole work of Redemption as key to the containment and organizing of Ordinary Time. It points to the victory of the cosmos over chaos, of life over death. The crenellated belt, an image of restraint and discipline, reinforced by the cross, image of the Redemption, laid out over the whole labyrinth, itself an image of the whole creation.
Conclusion
The labyrinth can therefore be seen as a very useful instrument to inculcate elements of astronomy and computation to students as well as to familiarize them with the mechanics of the liturgical year and help them memorize all this. Its structure accords well with the teaching methods based on memorization that Fulbert’s poem had emphasized and the whole body participation that was previously noted in the process of learning (Leclercq, 1982). The labyrinth also helps integrate the liturgical year with the elements of astronomy just so learned.
The question however may arise: If the purpose of the computus is to find the date of Easter and that of the movable feasts and that tables for up to 532 years ahead could be established, why bother with these arcane calculations and labyrinthine procedures? An interesting question that we address elsewhere.
The Chartres labyrinth is the only one among those of the French cathedrals to have a crown of cogs at its periphery and therefore which seems designed for computistical purposes. The others, such as the one at Amiens, for example, have generally the same design, though they are sometimes octagonal or even square rather than circular—they have four quadrants and twenty-eight hairpin turns—they do not seem to have other features that would suggest computistical work. They rather appear to be in the nature of architects’ seals on their creation, celebrating themselves and the founding bishops or be some traditional apotropaic devices.
It was the genius of the Chartrians to transform a symbol of often vague and obscure meaning into an instrument of mathematical precision and that was done simply by adding a crown of cleverly numbered cogs without in any way compromising the other possible meanings and functions of the labyrinth itself, in fact extending and deepening its significance.
Endnotes
(1) For people ever so slightly familiar with the astrolabe, a popular astronomical instrument in the twelfth century—Fulbert had written about it two centuries earlier—the presence of this marker could not be but a reminder of the “calculator” or “reckoner” which was “the small protruding tip on the outer rim of the spider at the beginning of the astrological sign of Capricorn.” (Anno Borst: The Ordering of Time. Chicago: University of Chicago Press, 1993, p. 59).
It would not therefore take extraordinary imagination to see that the signs of the zodiac and, with them, the months could be distributed around the periphery of the labyrinth transforming it into an annual calendar that could be adapted to the changing liturgical years.
(2) Alexander was born ca. 1170 in Ville Dieu (Normandy). The date of his death is unknown. He studied at the University of Paris and obtained the grade of (doctor Sorbonnibus). He was preceptor of the nephews of the bishop of Dol (Brittany) and became a canon in Avranche (Normandy). The Massa was composed around 1200.
(3) Ideally we would have 365/114 = 3.20 days per cup, since the crown of the labyrinth numbers 114 cups (including the virtual 2 at the entrance). In order to deal with whole numbers we shall assign 10 cups for each of the 7 months of 31 days, 9 for each of the 4 months of 30 days, and 8 for the month of 28 days for a total of (10 x 7) + (9 x 4) + 8 = 114 cups; strictly speaking, each cup will therefore represent: months of 31 days, 3.1 days; months of 30 days, 3 1/3 days; month of 28 days, 3 ½ days.
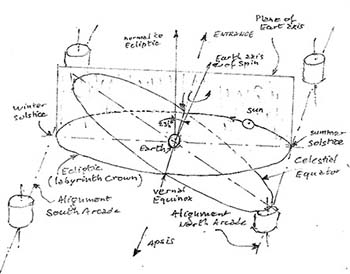
Note that in this view, the zodiac being represented by the fixed dented circumference, the earth, at the center of the labyrinth, has to be thought of as spinning on itself at the rate of one turn a day, anti-clockwise.
The earth’s axis of spin is then represented by a line contained in a vertical plane across the nave and going through the center of the labyrinth. Furthermore, this axis is inclined within that vertical plane from the perpendicular to the labyrinth by an angle of 23 ½ o towards the north arcade (summer solstice). This inclination represents the angle between the celestial equatorial plane and the plane of the ecliptic (see n. fig. 1).
(4) Van Wijk, 1936, verse 120. Commentary p. 100. The dates given in Bede’s solar calendar (Wallis, op. cit. Appendix 1, p. 379-391) based on Jones’s reconstructions are January 17: Aquarius; February 16: Pisces; March 18: Aries (First day of Creation); April 17: Taurus; May 18: Gemini; June 17: Cancer; July 18: Leo; August 18: Virgo; September 17: Libra; October 18: Scorpio; November 17: Sagittarius; December 18: Capricorn.
(5)The Moon phases analog:
A disk A (n. fig. 2) carrying the phases of the Moon with a Sun sign at its periphery next to the new Moon phase is cut out of paper or thin plastic.
A is placed over a representation of the periphery of the labyrinth bearing the Signs of the Zodiac, B (n. fig. 3) so that A can rotate with respect to the labyrinth center representing the Earth.
An additional Moon sign C (Fig. n.3.1) cut out of transparent thin plastic is placed on top of A. C, pivoting on the center of the labyrinth, moves along the circumference of the Moon phases. In Fig. 5 in the text showing the assembly it appears as a small circle within the Moon phases in Capricorn.
(6) Some may certainly object that there is no written evidence for such use of the labyrinth whereas we have at least some record of liturgical dances being performed on labyrinths in other churches (Auxerre, Sens). But as Wright (2001, 138-139) writes: “The documents are few in number, and with good reason...The dance of the labyrinth was on the margin of acceptable religious practice and the less said about it the better.” Further on he adds (p. 147): “Sometimes supposition is more satisfying to the spirit than documented fact—and intriguing allusion allows the historical imagination to roam more freely!” I couldn’t agree more.
And if, perchance, someone has a better idea to justify the specific mathematics of the labyrinth of Chartres, then, by all means, let the historical imagination roam ever more freely!
I find it piquant that Richard Holmes (The Age of Wonder. New York: Pantheon Books, 2009, p. 113) describes a similar sort of game organized in an English school early in the nineteenth century when enthusiasm for astronomy ran high after some of Herschel’s discoveries:
The young John Keats remembered an organized game at his school in Engfield,
in which all the boys whirled round the playground in a huge choreographed dance,
trying to imitate the entire solar system, including all the known moons (to which
Herschel had by then added considerably). Unlike Newton’s perfect brassy
clockwork mechanism, this schoolboy universe—complete with straying comets—
was a gloriously chaotic “human orrery’.
Keats did not recall the exact details, but one may imagine seven senior boy-planets
running round the central sun, while themselves being circled by smaller sprinting
moons (perhaps girls), and the whole frequently disrupted by rebel comets and
meteors flying across their orbits.
In any case, documents regarding teaching methods at Chartres are also rather scant. One can glean a few indications from the Metalogicon of John of Salisbury and from scattered remarks by alumni of Chartres in their own works (Herman of Corinthia, William of Conches...). But educational methodology as discourse for the record was evidently not a hot topic then.
( 7) Since the table of the nineteen-year cycle started with year 1 and did not account for that “Moon jump” of year 0 which, itself, was not included in the series of cycles and since this was never corrected, calculation must be based on March 22nd, as the earliest acceptable date for Easter. This, repeating every 19 years, allows only 19 possible dates for the ecclesiastic full Moons after March 21st.
(8) The following is adapted from the commentary by F. Wallis, op. cit., pp. 295-297.
(9) Counting backward to January 1st, the age of the Moon is therefore found to be 9. Nine, then, is the January lunar regular. January has thirty lunar days but thirty-one calendar days, so that the Moon on February 1st will be older by one day than it was on January 1st. The February lunar regular is therefore 9 + 1 = 10. Continuing forward, since February has 29 lunar days and 28 calendar days in common years, the Moon on March 1st will be one day younger than on February 1st. Therefore 9 will be the March lunar regular so that March 21st corresponds to 21 + 9 = 30, i.e. the end of the third lunar month, and March 22nd, will be the beginning of the new lunar month, i.e. the New Moon. One proceeds in the same fashion through the remaining months of the year.
(10) As was seen previously, the lunar year has 29.5 x 12 = 354 days and the solar year 365 days, a difference of 11 days. On the first day of the second year of the 19-year cycle, the age of the moon is therefore 11 days older than it was on the first day of the first year. Each new year will add similarly 11 to the age of the Moon. When this number exceeds 30, 30 must be subtracted, since that is the number of days in the so-called embolismic month that is added occasionally to compensate for the difference.
(11) The 28-year solar cycle is designed so as to begin on a leap year. It will therefore be constituted of seven sequences of four years, each sequence made up of one initial leap year followed by three common years. Following Roman custom, the extra leap day is introduced on the 24th of February so that there will be two February 24ths that year. The result of introducing the leap day is that all week days after that date will be shifted forward by one, e.g. if March 1st of the year preceding the leap year is a Monday, then March 1st for the leap year will be a Wednesday instead of a Tuesday if it were a common year.
In the lunar case, March 22nd was chosen as a reference point for the calculation of the epact (New Moon, epact 0). For the solar case, February 24th would constitute a natural reference point, since this is where the extra day of the leap year was inserted. However, being interested here in weekdays occurring in cycles of 7, and noting that March 24 always occurs on the same weekday as February 24, March 24 is chosen in preference as it falls within the period of the Easter reckoning and is therefore computistically more convenient.
(12) For instance, between April 1st (i.e. March 32nd; 31 + 1) and March 24, there are eight days (32 – 24 = 8) and therefore the weekday of April 1st will be shifted forward by one day, since 8 – 7 = 1. The solar regular for April is therefore 1. Similarly for May, we have between March 24th and May 1st: 8 + 30 = 38 days and therefore a solar regular of 38 mod 7 = 3 proceeding similarly for all other months, we obtain the following table:
TABLE 1: Monthly or Solar Regulars
1st of the month |
Calculation |
Monthly Regular |
April |
0 + 1 = |
1 |
May |
1 + 2 = |
3 |
June |
3 + 3 = |
6 |
July |
6 + 2 = 7 + 1 = 0 + 1 = |
1 |
August |
1 + 3 = |
4 |
September |
4 + 3 = |
7 |
October |
0 + 2 = |
2 |
November |
2 + 3 = |
5 |
December |
5 + 2 = |
7 |
January |
0 + 3 = |
3 |
February |
3 + 3 = |
6 |
March |
6 – 1 = |
5 |
|
|
|
For March, we subtract 1 because February has 28 days only and eliminating March 1st because it was included in a previous count so that we have 6 + 28 -1 equivalent to 6 + 0 -1 = 6 – 1 = 5.
(13) Dionysius Exiguus, who designed the system, chose to start the first cycle on year 20 AD, the first year of that cycle being a leap year beginning on a Tuesday, January 1st. Since weekdays repeat from 28-year cycle to 28-year cycle without a shift, the solar epact, i.e. the shift in weekdays due to the previous cycle will be 0. However, the first year of the cycle being a leap year will introduce a shift of one day in the succession of week days. The solar epact or concurrent for the first year will therefore be 1. The next three common years following will each add one weekday shift, since 365/7 = 52, remainder 1. And their concurrents will be 2,3, and 4 respectively. The fifth year will again be a leap year. This year will add a shift of 2 (1 for the 365th day and another for the leap day). The concurrent for the fifth year will therefore be 4 + 2 = 6, etc. Since we are dealing with weekdays, i.e. cycles of 7, we must subtract 7 from any number exceeding 7 until it is reduced to 7 or less. We can therefore readily draw a table of
yearly concurrents as shown:
TABLE 2. Solar Epacts or Concurrents (L= Leap Year; C = Common Year)
Rank of Year in Seq. → |
1 |
2 |
3 |
4 |
Rank of Seq. in Cycle |
L |
C |
C |
C |
1 |
1 |
2 |
3 |
4 |
2 |
6 |
7 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
4 |
2 |
3 |
4 |
5 |
5 |
7 |
1 |
2 |
3 |
6 |
5 |
6 |
7 |
1 |
7 |
3 |
4 |
5 |
6 |
(14) Note that the concurrent for any given year can be obtained by simple modular arithmetic. Take the year 1194: since the system of solar cycles starts with year 20 AD and Brother Exiguus did not provide for a year 0 AD, the cycle being one of 28 years, we simply write
(1194 – 20 + 1) mod 28
or (1194 – 19) mod 28 = 27.
This gives us the rank of the year 1194 AD in its 28-year cycle. The concurrent will therefore be found in Table 2 (Note 11) in the twenty-seventh position, i.e. on the seventh row and the third column and we see that it is indeed 5.
(15) In modular arithmetic the result is the remainder of the division of the dividend by the divisor, neglecting the quotient, which is kept as a whole number.
(16) The notation Y/4] indicates that number Y is divided by 4 but the one-sided square bracket, ] , specifies that the quotient must remain a whole number. In other words, the operation stops as soon as the remainder becomes less than the divisor.
(17) The date of April 10, 1194 for Easter Sunday in the Julian calendar can be confirmed by recourse to the “Easter calculator” at http://www.ortelius.de/kalender/form_en2.php
or by looking up Tables 3 and 4.
(18) I cannot resist here quoting from an article in the September 5, 2008 New York Times Science Section: “For the Brain Remembering is Like Reliving” by Benedict Carey:
In studies of rodents...neuroscientists have shown that special cells in the hippocampus
are sensitive to location, activating when the animal passes a certain spot in the maze.
The firing pattern of these cells forms the animal’s spatial memory and can predict which
way the animal will turn, even if it makes a wrong move... Some scientists argue that as
humans evolved, these same cells adapted to register a longer list of elements—including,
possibly, sounds, smells, time of the day, and chronology—when an experience occurred
in relation to others.
(19) That Easter occurs on the 64th day of the cycle is, of course, very significant, since 64 = 8 x 9, an octave of octaves marking the most total completion imaginable. Furthermore, 6 + 4 =10, another perfection
Works Cited
Bede. (1990). Ecclesiastical History of the English People. London, UK: Penguin Books.
Behrends, F. (1976). The Letters and Poems of Fulbert of Chartres. Oxford: Clarendon Press.
Carruthers, M. (1998). The Craft of Thought: Meditation, Rhetoric, and the Making of Images, 400-1200. Cambridge, UK: Cambridge University Press.
Critchlow, K. (1982). Time Stands Still: New Light on Megalithic Science. New York: St. Martin’s Press.
Doob, P. R. (1990). The Idea of the Labyrinth. Ithaca, NY: Cornell University Press.
Hawkins, G.S. (1993). Stonehenge Decoded. New York: Barnes and Noble.
Heath, R. (1998). Sun, Moon, and Stonehenge. Cardigan, Wales: Bluestone Press.
Heath, R. (2001). Sun, Moon, and Earth. New York: Walker and Company.
Heilbron, J. (2001). The Sun in the Church: Cathedrals as Solar Observatories. Cambridge, MA: Harvard University Press.
James, J. (1982). Chartres, Les constructeurs. Chartres: Soc. Arch. d’E. & L.
Leclercq, J. (1982). The Love of Learning and the Desire for God: The Study of Monastic Culture. New York: Fordham University Press.
McCluskey, S. C. (1998). Astronomies and Cultures in Early Medieval Europe. New York: Cambridge University Press.
Thom, A. (1967). Megalithic Sites in Britain. Oxford, UK: Oxford University Press.
Thomas, M. (1979). L’age d’or de l’enluminure:Jean de France, duc de Berry, et son temps. Paris: Editions Vilo.
Van Wijk, W.E. (1936). Le nombre d’or: Etude de chronologie technique suivie du texte de la Massa Compoti d’Alexandre de Villedieu avec Traduction et Commentaire. La Haye: Martinus Nijhoff.
Wallis, F. (1999). Bede: The Reckoning of Time, translated with introduction, notes and commentary. Liverpool University Press.
Wright, C. (2001). The Maze and the Warrior. Cambridge, MA: Harvard University Press.
Figure Illustrations

Fig. 1 The Labyrinth of Chartres
Notice entrance at bottom of figure with space to accommodate an additional cog; also, at a quarter turn to the right, presence of a marker in the outer ring. The labyrinth entrance indicates the west and the marker, the south.
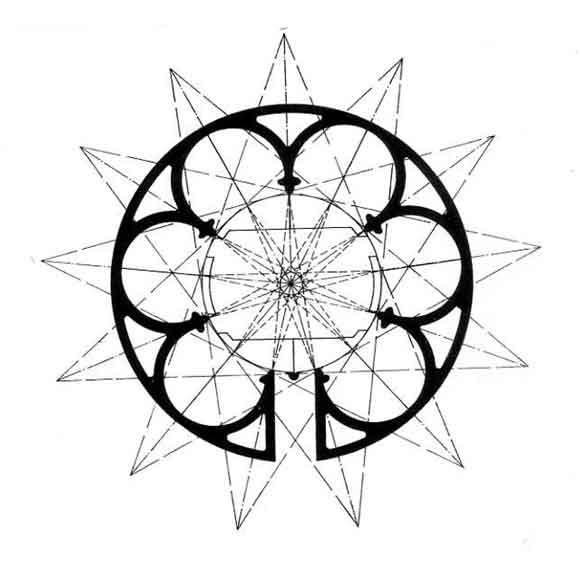
Fig. 2. Center of the Chartres Labyrinth and its Geometry
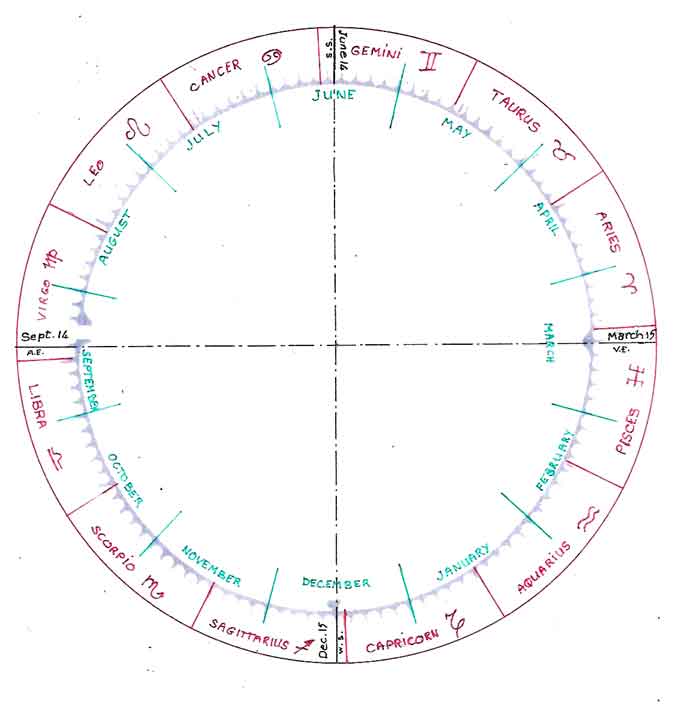
Fig. 3 Calendrical Aspect of the Labyrinth
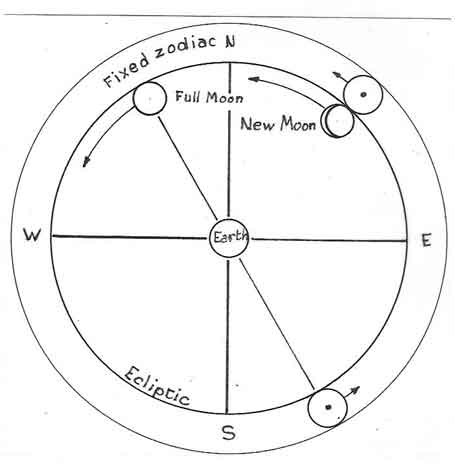
Fig. 4. New Moon/Full Moon
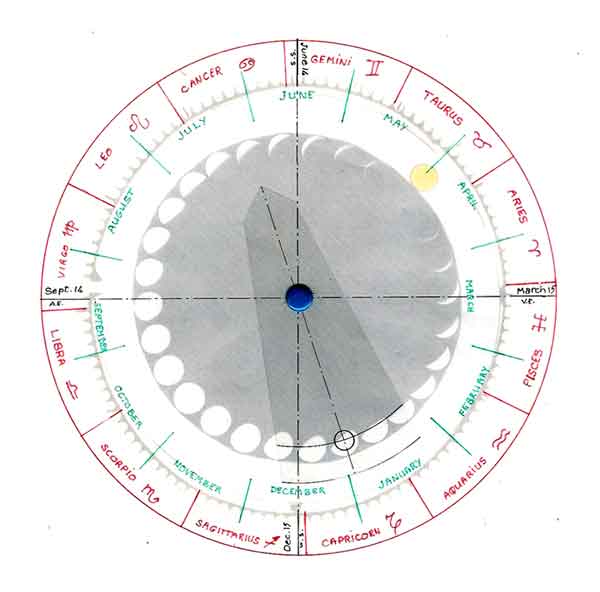
Fig. 5 Moon Phase Analog
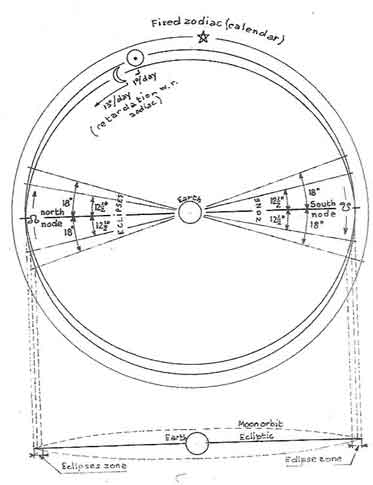
Fig. 6 Eclipse Zones
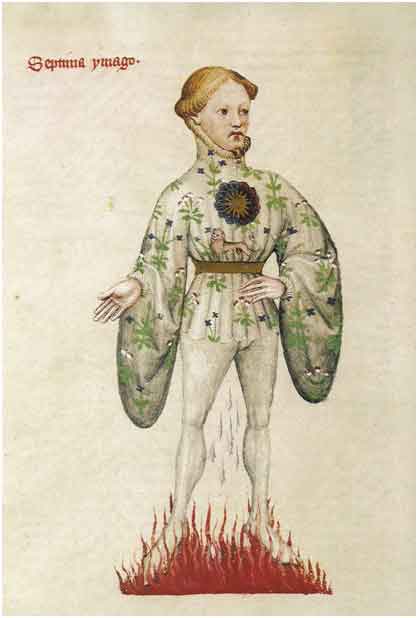
Fig. 7 a. The Boy-Sun
Though dating from the turn of the 15th century, this handsome Boy-Sun, which appeared in John Foxton’s Liber Cosmographiae of 1408 could not look much different from what fashion designers at the turn of the 13th century might have been able to do for young Chartrians. The seven last pictures of the Cosmographiae are devoted to the seven planets then known. They are represented as human characters whose clothes carry emblems of the planets, like the radiating golden sun on the chest of the young man here, as well as a symbol of the corresponding zodiac sign, viz. the Lion, in our case. The flames around the feet of the young man, which do not appear to burn him, are a reminder of the nature of the sun, giver of heat and light.
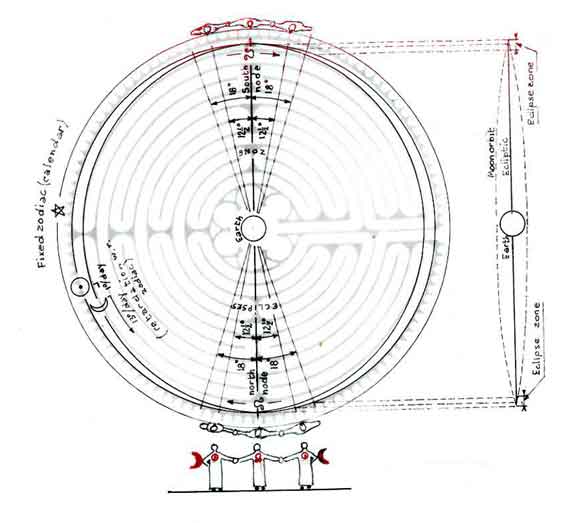
Fig. 7. The Dance of the Eclipses.
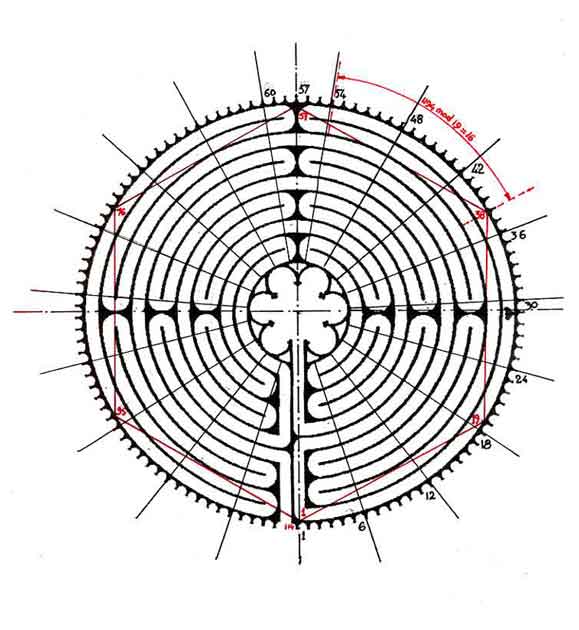
Fig. 8. Determining the Golden Number
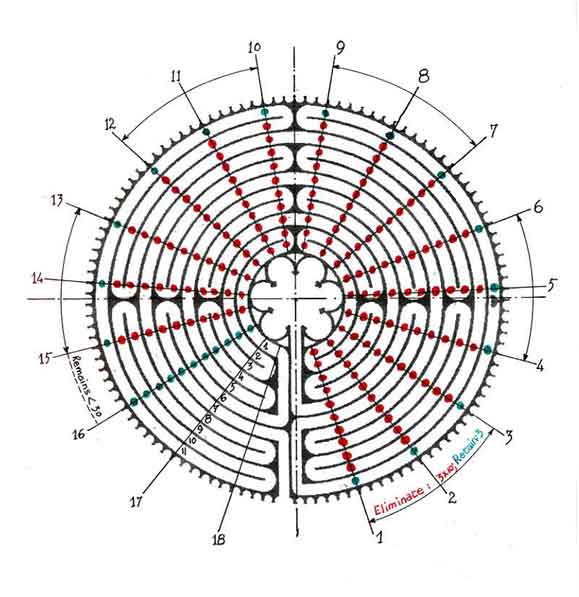
Fig. 9. Finding the Lunar Epact
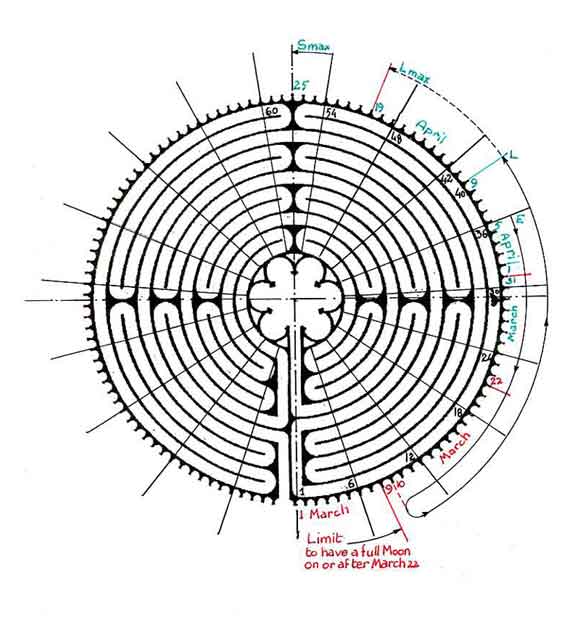
Fig.10. Finding the Easter Limit
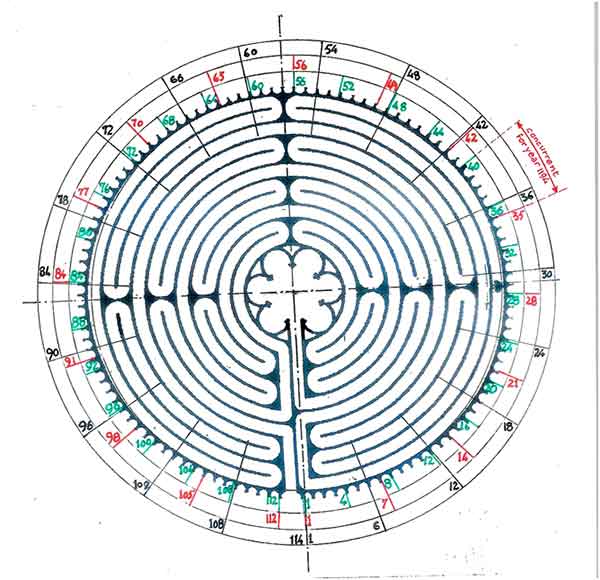
Fig. 11 Determining the Concurrents
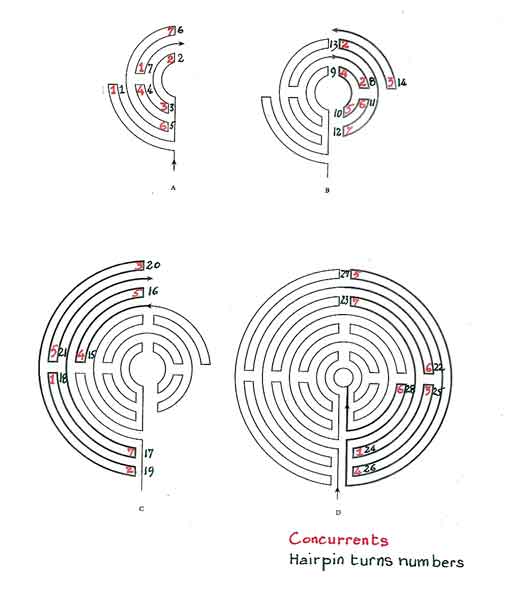
Fig. 12 Alternative Determination of the Concurrents
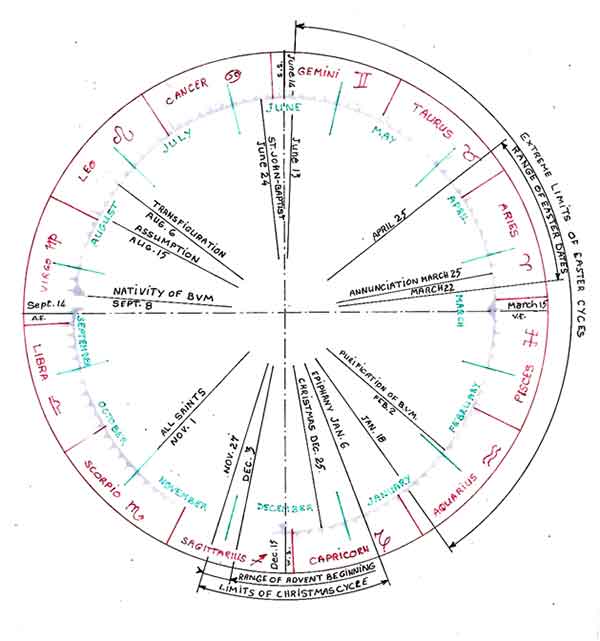
Fig. 13 The Liturgical Year
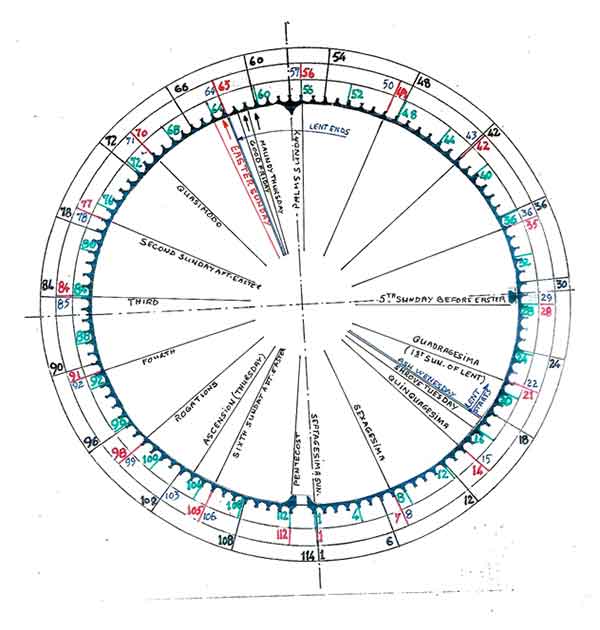
Fig. 14 The Cycle of Easter
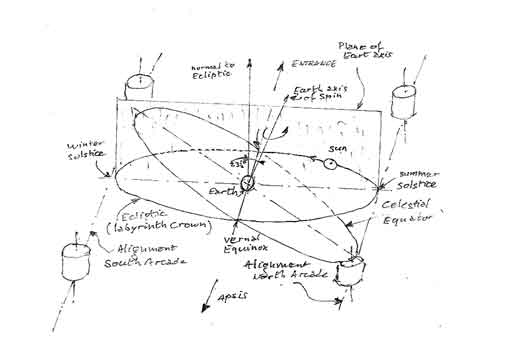
n. fig. 1 Visualization of the Earth Axis of Spin
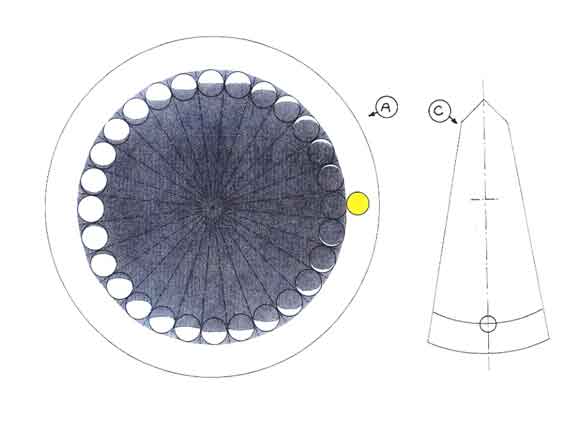
n. fig. 2 Elements A and C of Moon Phase Analog
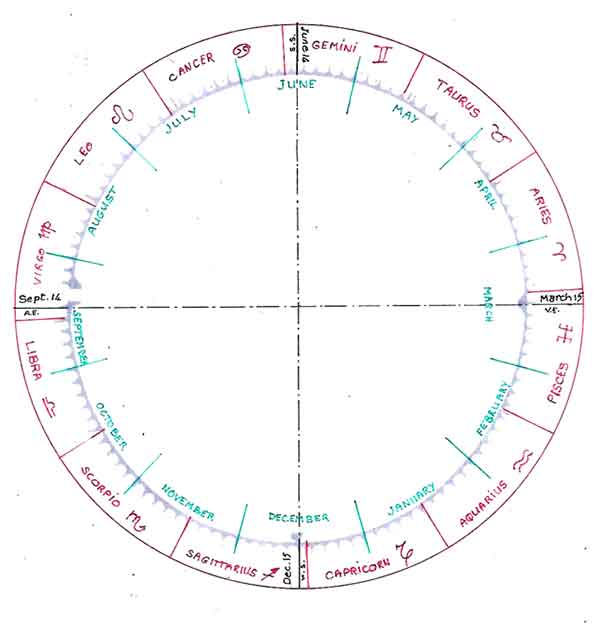
n. fig. 3 Element B of the Moon Phase Analog